√1000以上 多角形の角の大きさの和 301116-多角形の角の大きさの和の求め方
正 多 角形 の 内角 の 和 簡単公式 五角形の内角の和を3秒で計算できる方法 Stg Origin Aegpresents Com
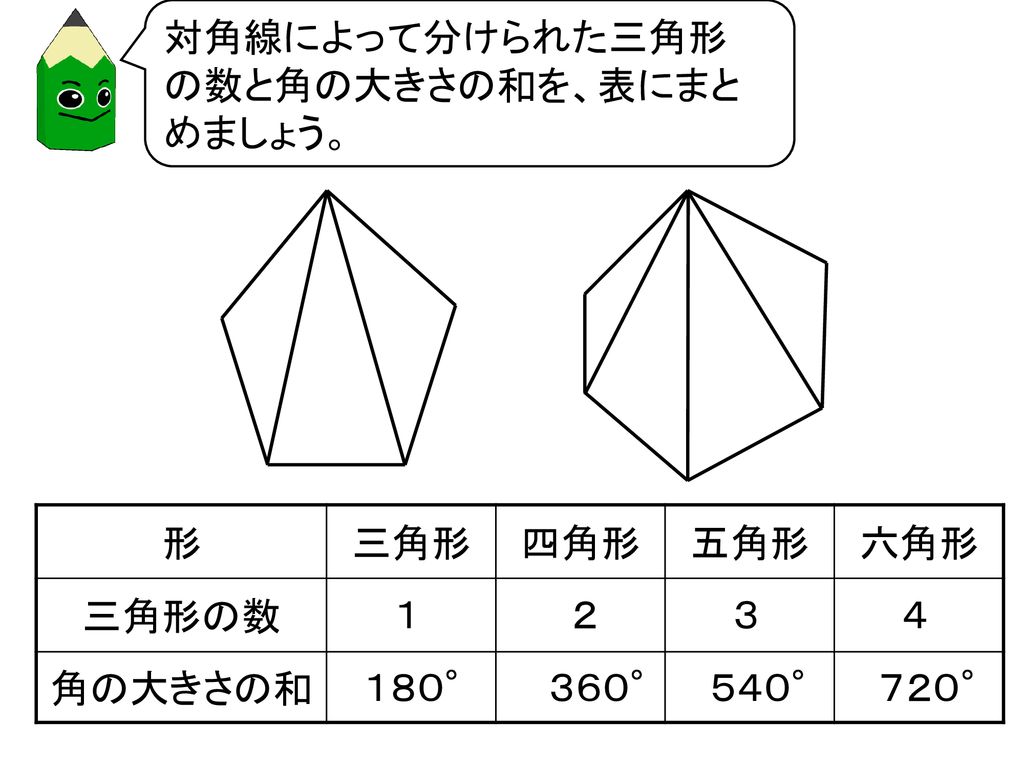
多角形の角の大きさの和 Type of schools Elementary School Authorized year 19 Subject area Arithmetic Subject Arithmetic Target grade 5 Course Of Study Item (Label) B（1）ア（イ） 三多角形の内角の和は 180°× (n−2) 正多角形のすべての内角の大きさは等しいから,正n角形の1つの内角の大きさは (n−2)×180°nnnnnnnnnnn =180°− 360°nnnnn 例 • 正三角形 外角= 360°3nnnn =1°
多角形の角の大きさの和の求め方
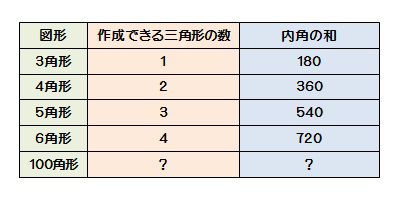
多角形の角の大きさの和の求め方-多角形の内角の和は 180°× (n−2) 正多角形のすべての内角の大きさは等しいから,正n角形の1つの内角の大きさは (n−2)×180°nnnnnnnnnnn =180°− 360°nnnnn 例 • 正三角形 外角= 360°3nnnn =1°（3） けんさんが，四角形の4つの角の大きさの和を求めた考え方で，五角形の5つの角 の大きさの和を求めましょう。 図3のように点Pとそれぞれの頂点を点で結び三角形に分けて考え ると，四角形
多角形の内角の和 は何度なのか を説明します おかわりドリル
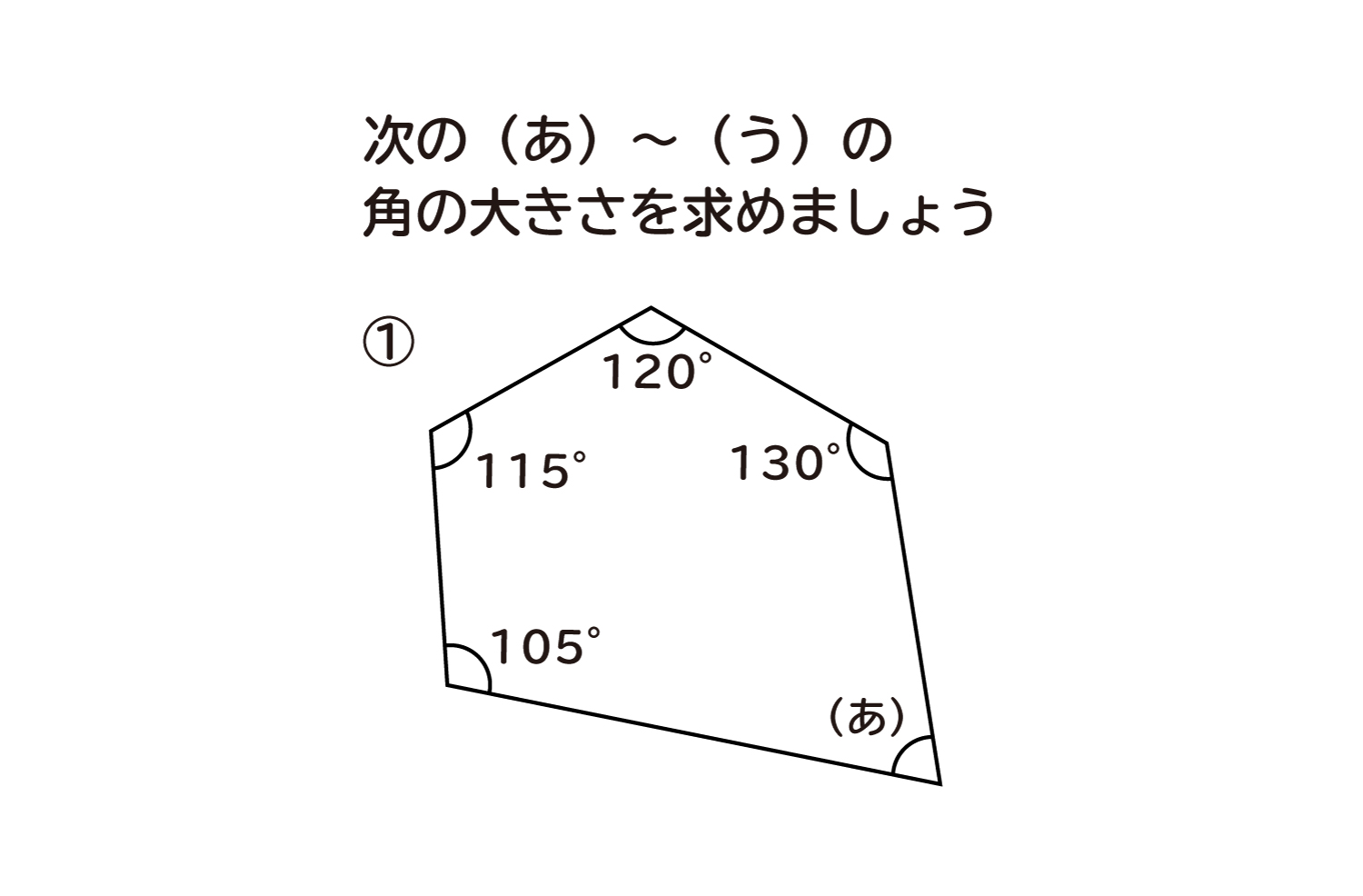
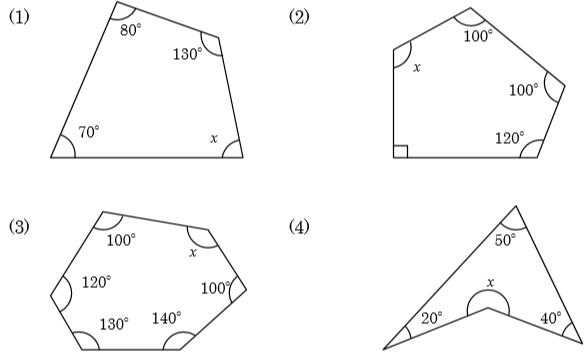
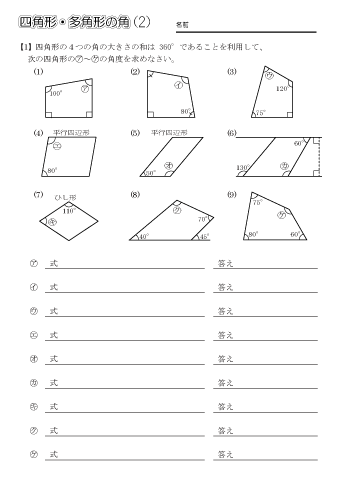
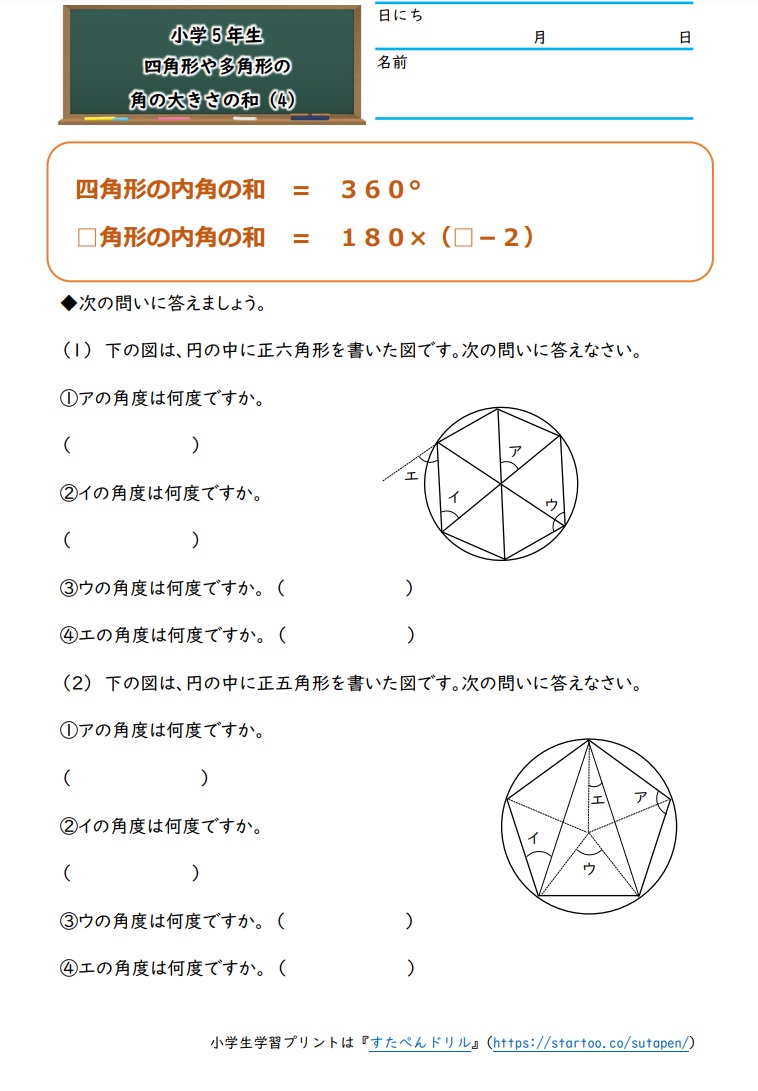
小学校5年生の角の問題を教えてください。 どうしてもわかりません。 次の図で四角形アイウエはひし形、三角形オイウは正三角形です。あの角度を計算で求めこたえを( )に書きま1 次の多角形の角の大きさの和を求めましょう。 ① ① 五角形の内角の和は ② 答え： 2 次の図で、㋐・㋑の角度は何度ですか。計算で求めましょう。 ㋐= 答え： ② 六角形の内角の和は ㋑= 答え： ⑪ 回答 さつき (*´˘`*)♡ (辞めました) 1年以上前 これは公式でも求めれるよ〜 n角形の内角の和= (n2)×180 0 💫ねお💫 1年以上前 ありがとうございます 0
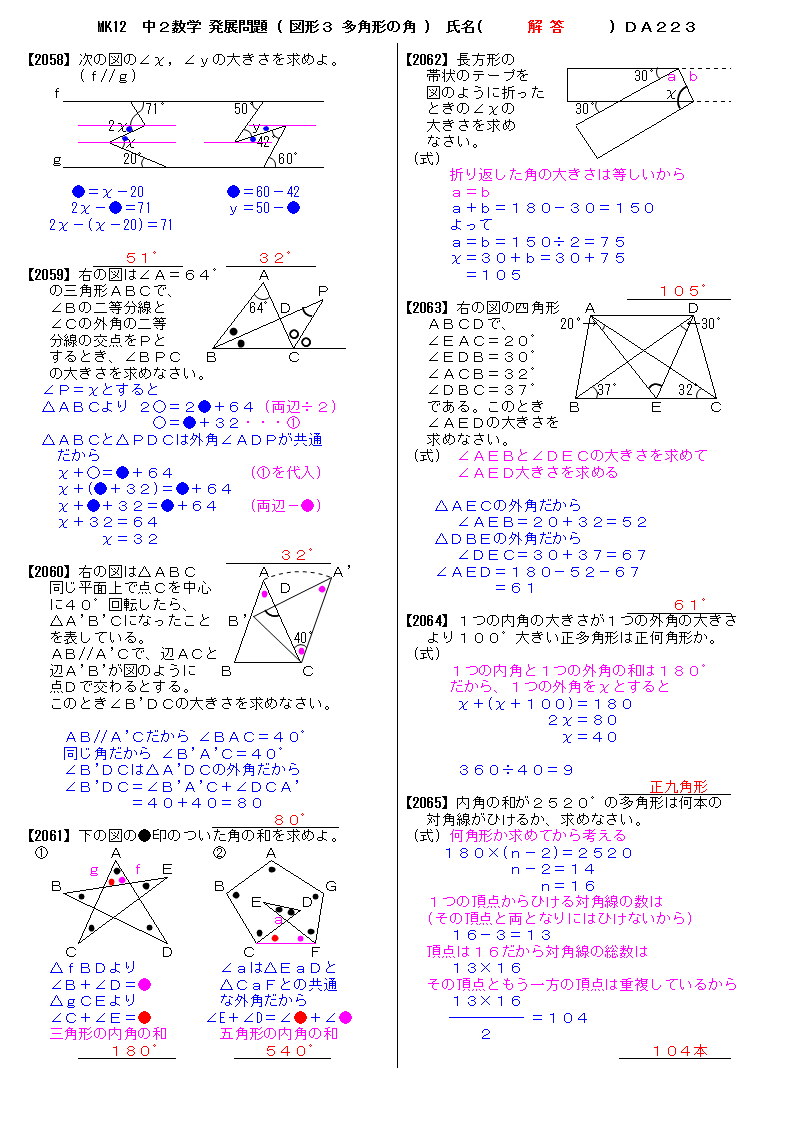
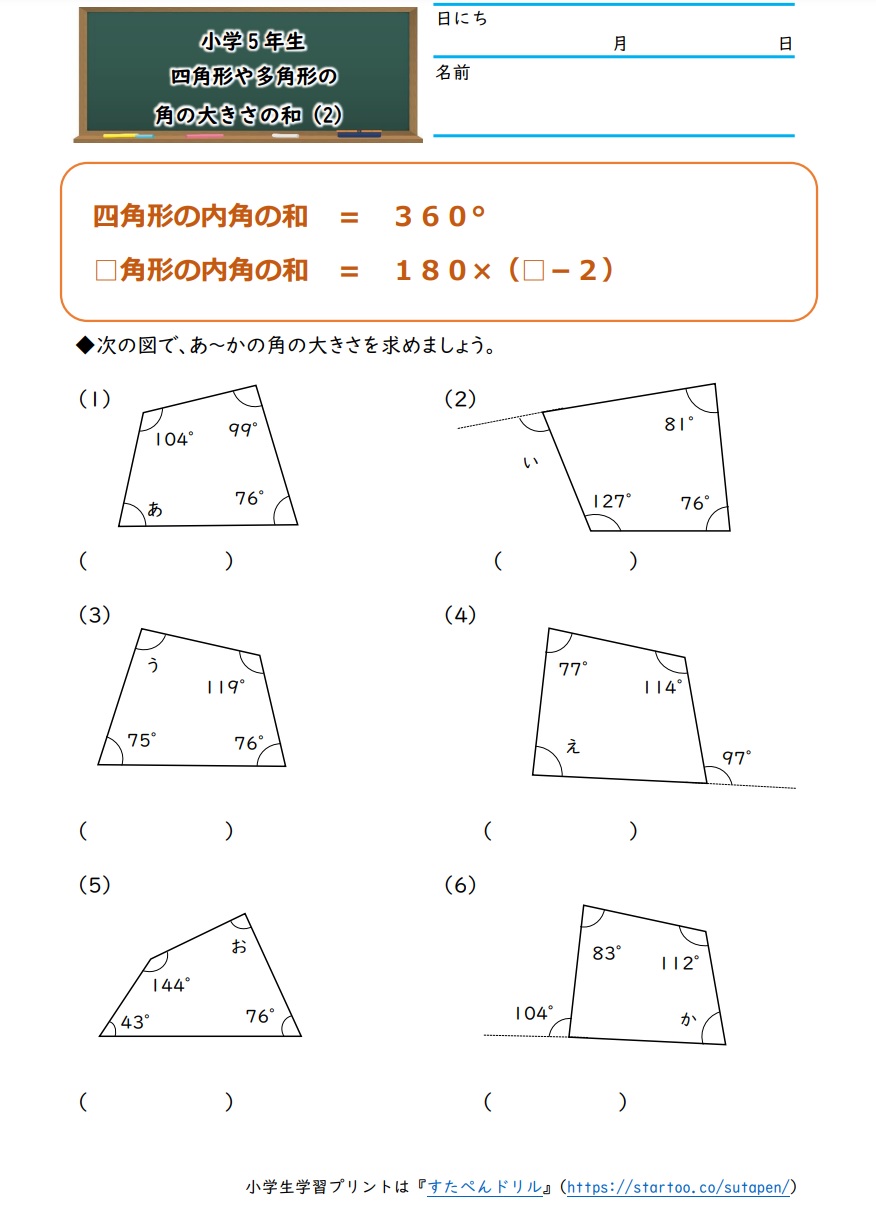
四角形 五角形 六角形 七角形 八角形 にあてはまる数字を答えましょう。 四角形や多角形の角の大きさの和 名前 日にち 月 日 小学5年生 次の多角形の角の大きさの和を求めましょう。 （1）8 本の直線上の事実は次のように説明できます． まず， 多角形の各頂点における内角と一つの外角の和は常に 180° 180 ° なので， n n 角形の内角と外角の和の合計は， 180°×n 180 ° × n です．そして， n n 角 正多角形とは、すべての辺、角の大きさが等しい多角形のことをいいます。 つまり、 正多角形の1つ分の内角は、内角の和を等分することで求めれます。 例 (正三角形) 内角の
多角形の角の大きさの和の求め方のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 特別な多角形の内角の和 まなびの学園 | 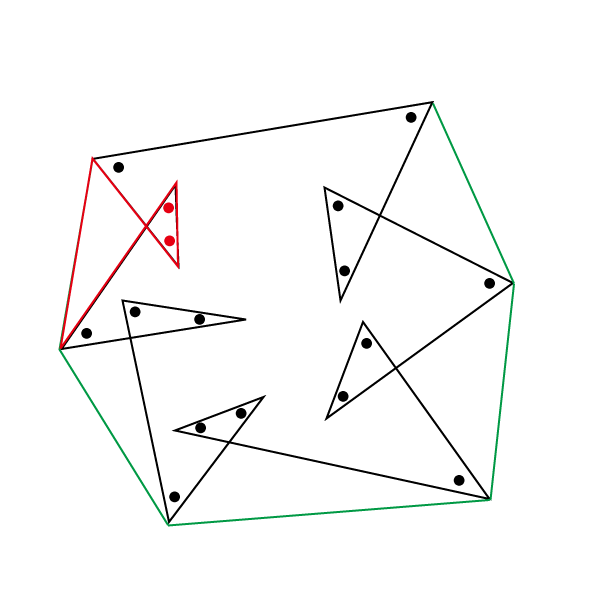 特別な多角形の内角の和 まなびの学園 | 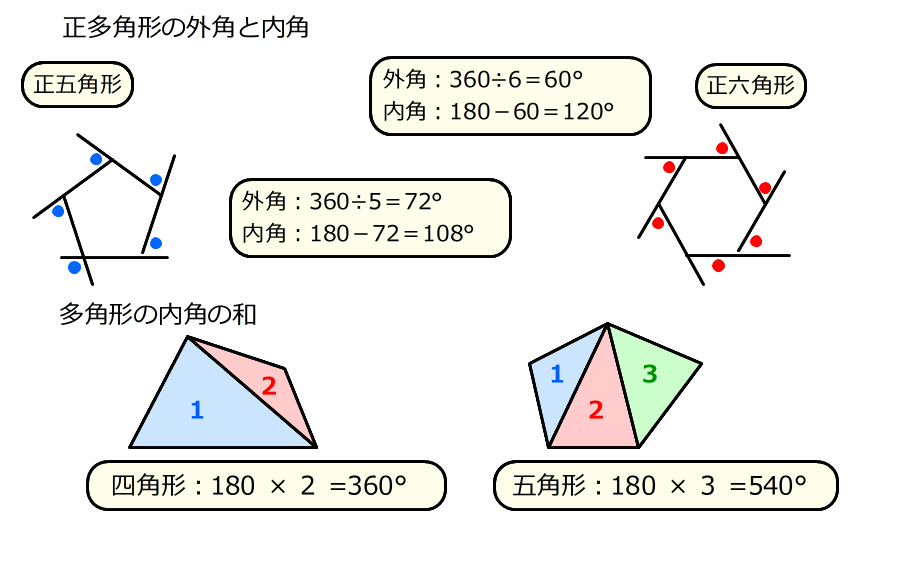 特別な多角形の内角の和 まなびの学園 |
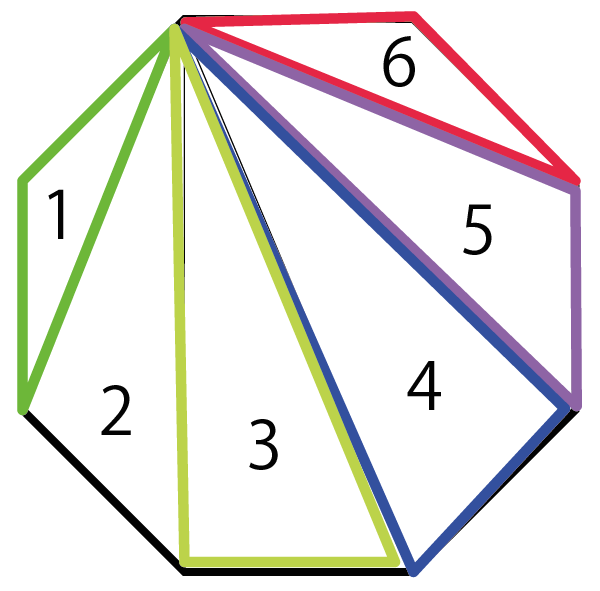 特別な多角形の内角の和 まなびの学園 |  特別な多角形の内角の和 まなびの学園 |  特別な多角形の内角の和 まなびの学園 |
 特別な多角形の内角の和 まなびの学園 | 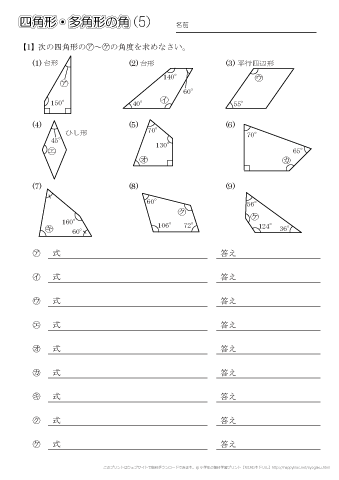 特別な多角形の内角の和 まなびの学園 |  特別な多角形の内角の和 まなびの学園 |
「多角形の角の大きさの和の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 特別な多角形の内角の和 まなびの学園 |  特別な多角形の内角の和 まなびの学園 |  特別な多角形の内角の和 まなびの学園 |
 特別な多角形の内角の和 まなびの学園 | 特別な多角形の内角の和 まなびの学園 |  特別な多角形の内角の和 まなびの学園 |
 特別な多角形の内角の和 まなびの学園 |  特別な多角形の内角の和 まなびの学園 |  特別な多角形の内角の和 まなびの学園 |
「多角形の角の大きさの和の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 特別な多角形の内角の和 まなびの学園 |  特別な多角形の内角の和 まなびの学園 |  特別な多角形の内角の和 まなびの学園 |
 特別な多角形の内角の和 まなびの学園 |  特別な多角形の内角の和 まなびの学園 | 特別な多角形の内角の和 まなびの学園 |
 特別な多角形の内角の和 まなびの学園 |  特別な多角形の内角の和 まなびの学園 |  特別な多角形の内角の和 まなびの学園 |
「多角形の角の大きさの和の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 特別な多角形の内角の和 まなびの学園 |  特別な多角形の内角の和 まなびの学園 |  特別な多角形の内角の和 まなびの学園 |
特別な多角形の内角の和 まなびの学園 |  特別な多角形の内角の和 まなびの学園 |  特別な多角形の内角の和 まなびの学園 |
 特別な多角形の内角の和 まなびの学園 |  特別な多角形の内角の和 まなびの学園 | 特別な多角形の内角の和 まなびの学園 |
「多角形の角の大きさの和の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 特別な多角形の内角の和 まなびの学園 |  特別な多角形の内角の和 まなびの学園 |  特別な多角形の内角の和 まなびの学園 |
 特別な多角形の内角の和 まなびの学園 |  特別な多角形の内角の和 まなびの学園 |  特別な多角形の内角の和 まなびの学園 |
特別な多角形の内角の和 まなびの学園 |  特別な多角形の内角の和 まなびの学園 |  特別な多角形の内角の和 まなびの学園 |
「多角形の角の大きさの和の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
特別な多角形の内角の和 まなびの学園 |  特別な多角形の内角の和 まなびの学園 |  特別な多角形の内角の和 まなびの学園 |
 特別な多角形の内角の和 まなびの学園 | 特別な多角形の内角の和 まなびの学園 |  特別な多角形の内角の和 まなびの学園 |
 特別な多角形の内角の和 まなびの学園 |  特別な多角形の内角の和 まなびの学園 |  特別な多角形の内角の和 まなびの学園 |
「多角形の角の大きさの和の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 特別な多角形の内角の和 まなびの学園 | 特別な多角形の内角の和 まなびの学園 |  特別な多角形の内角の和 まなびの学園 |
 特別な多角形の内角の和 まなびの学園 |  特別な多角形の内角の和 まなびの学園 |  特別な多角形の内角の和 まなびの学園 |
 特別な多角形の内角の和 まなびの学園 |  特別な多角形の内角の和 まなびの学園 |  特別な多角形の内角の和 まなびの学園 |
「多角形の角の大きさの和の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 特別な多角形の内角の和 まなびの学園 |  特別な多角形の内角の和 まなびの学園 |  特別な多角形の内角の和 まなびの学園 |
 特別な多角形の内角の和 まなびの学園 |  特別な多角形の内角の和 まなびの学園 |  特別な多角形の内角の和 まなびの学園 |
 特別な多角形の内角の和 まなびの学園 |  特別な多角形の内角の和 まなびの学園 |  特別な多角形の内角の和 まなびの学園 |
「多角形の角の大きさの和の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
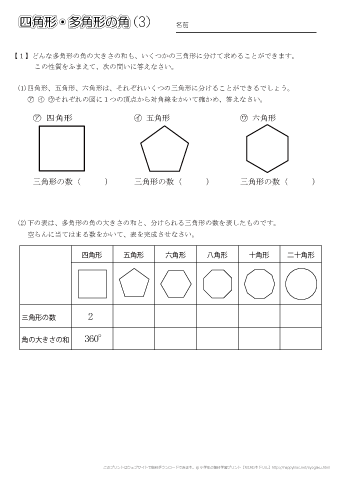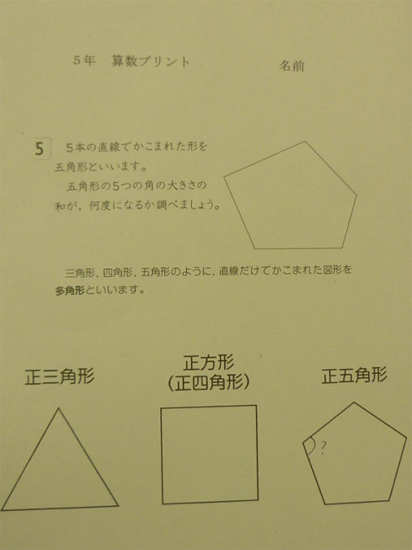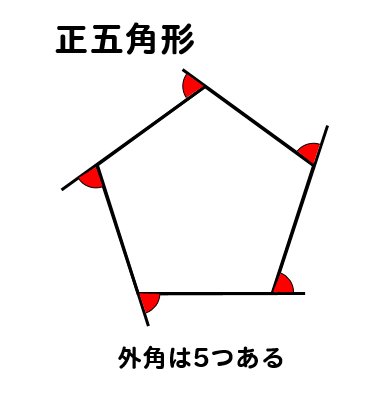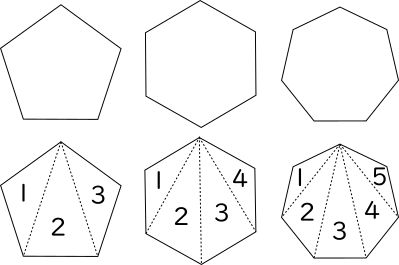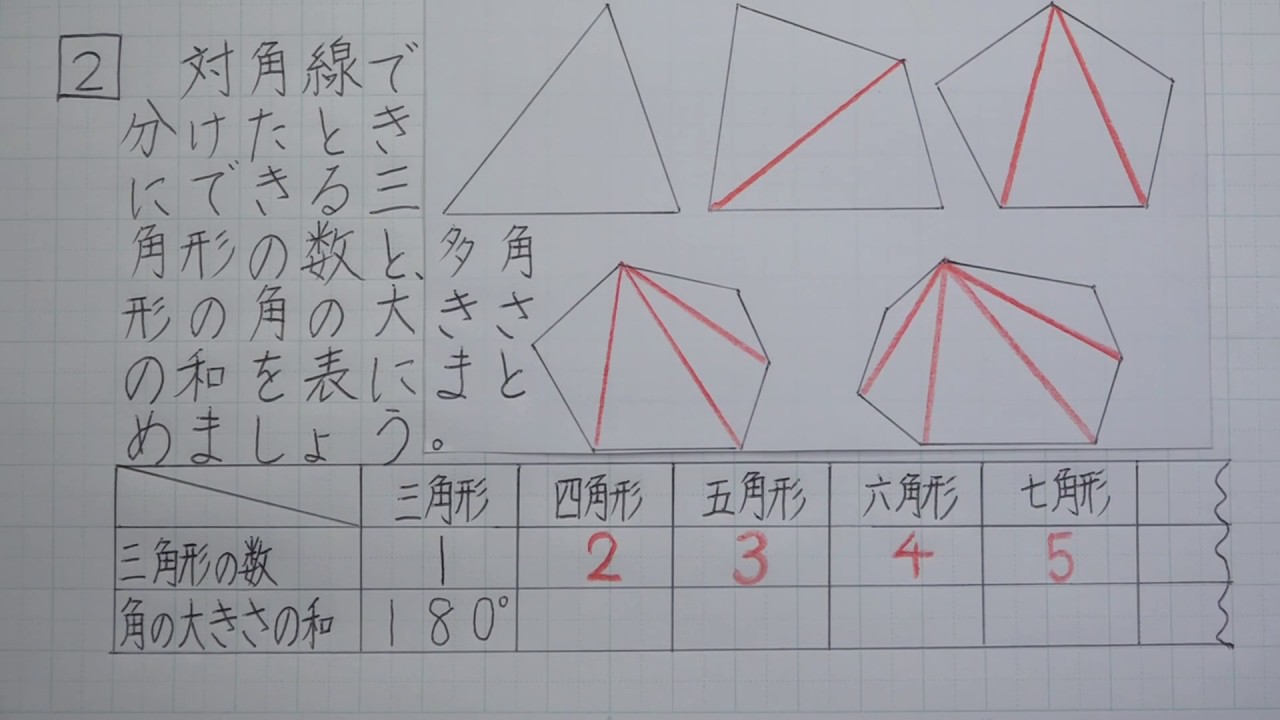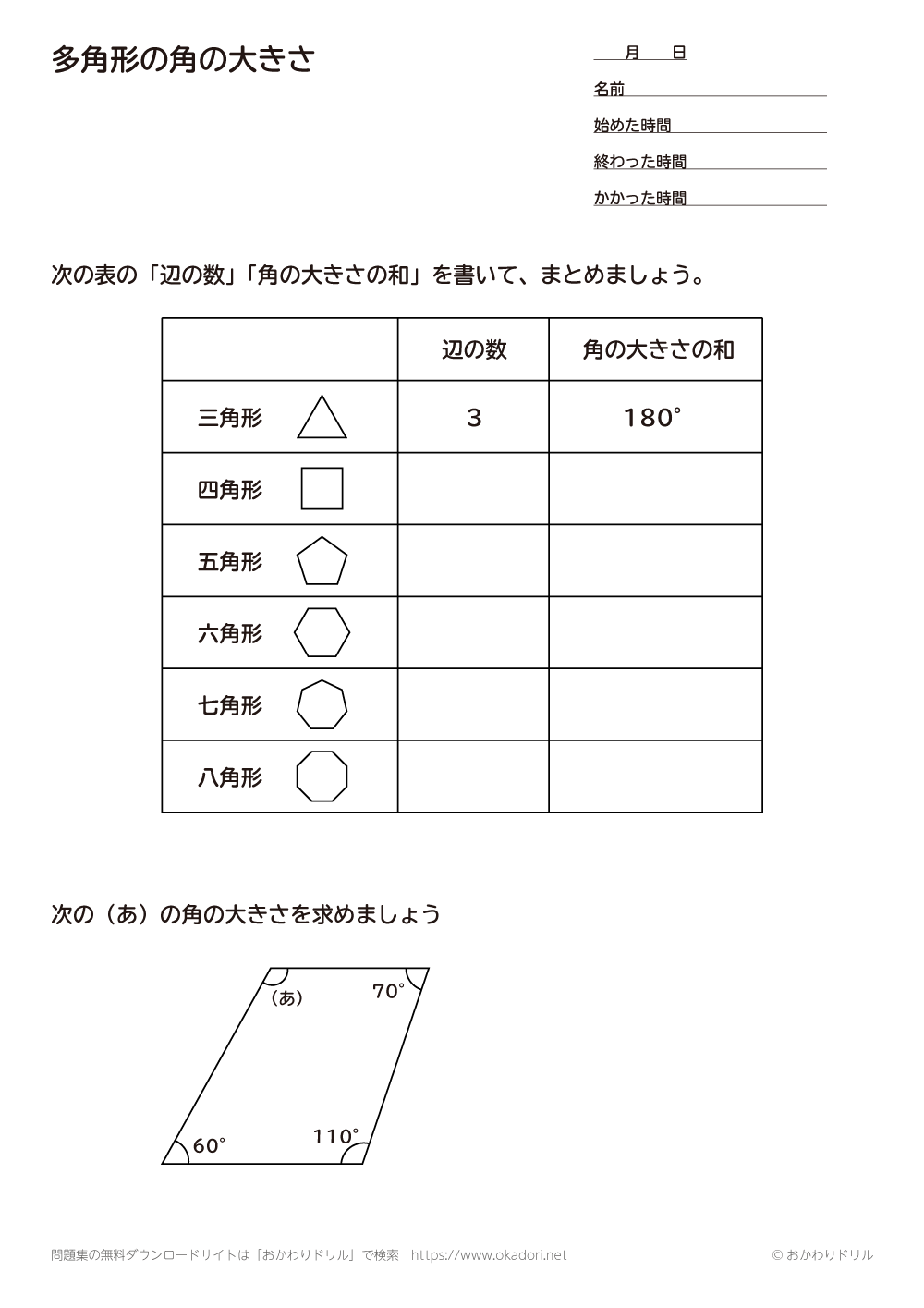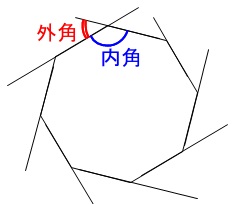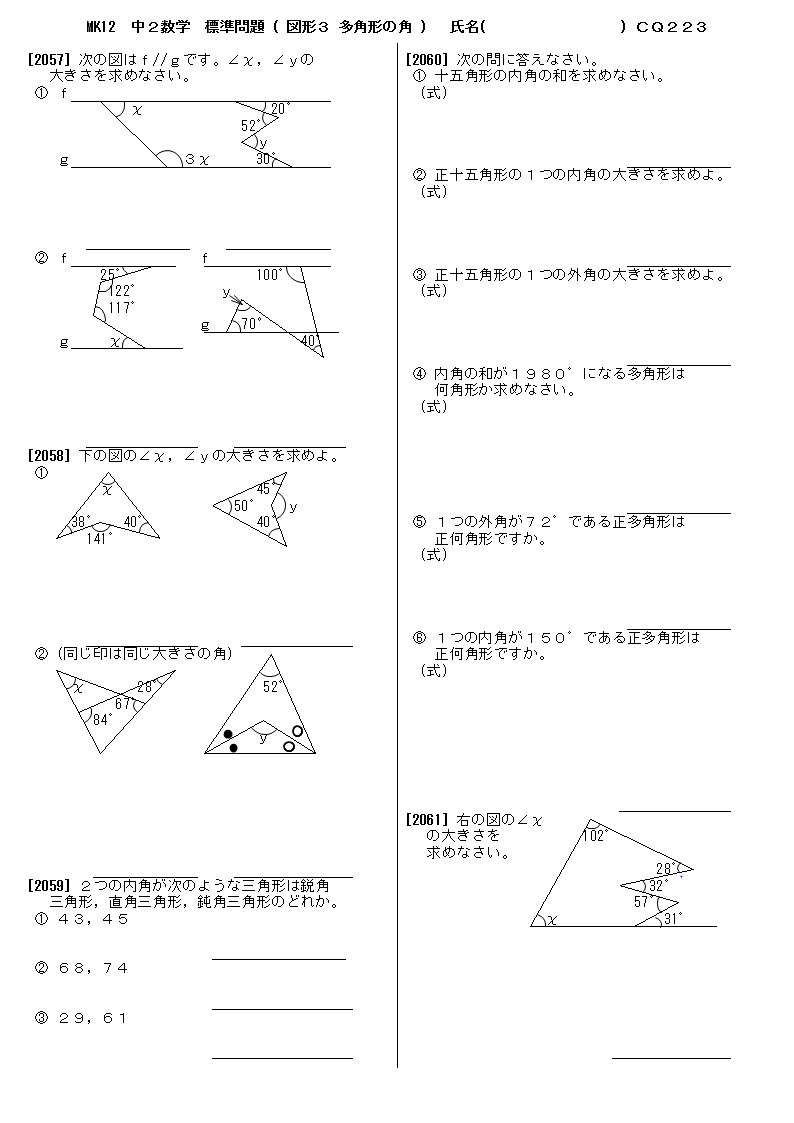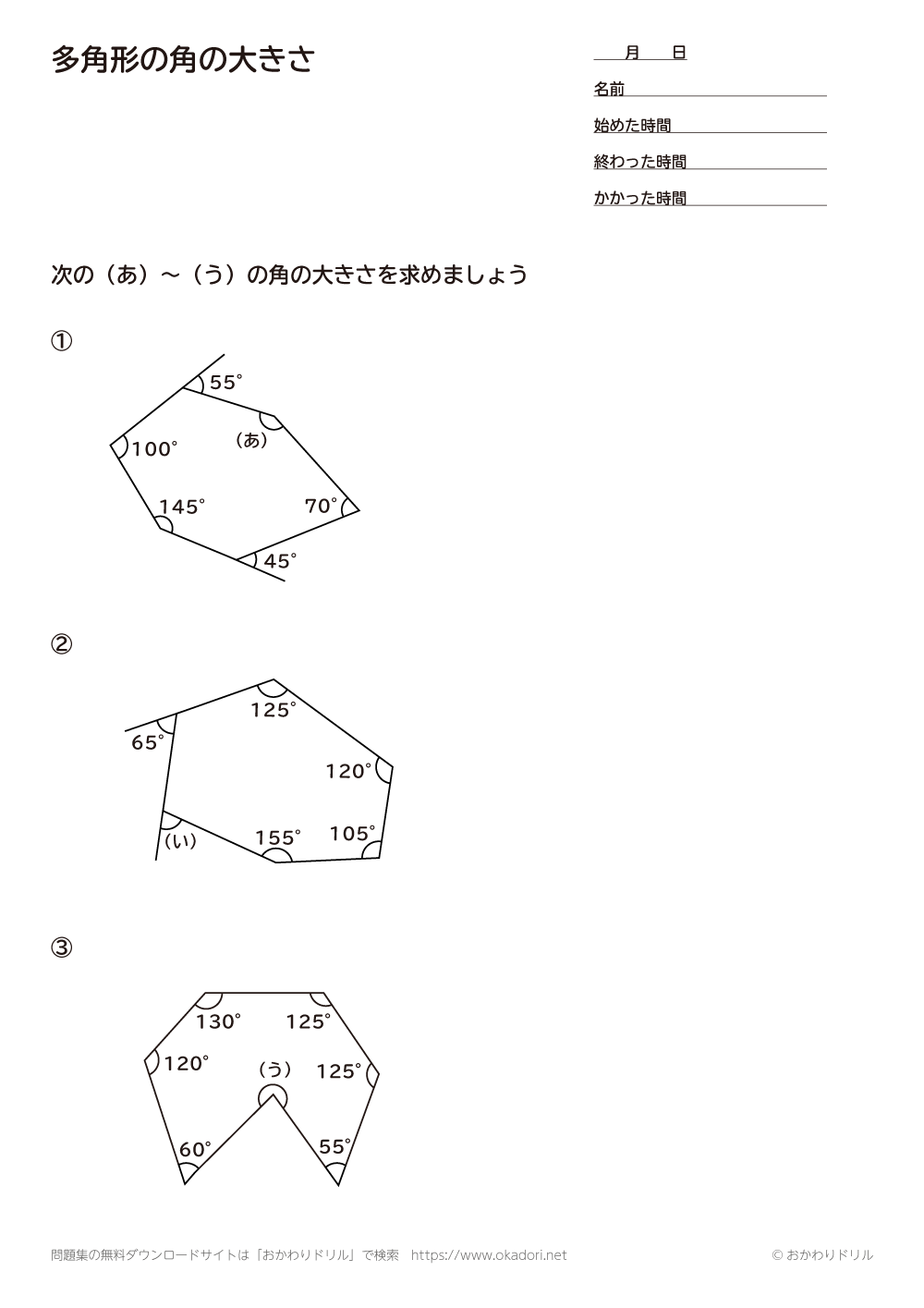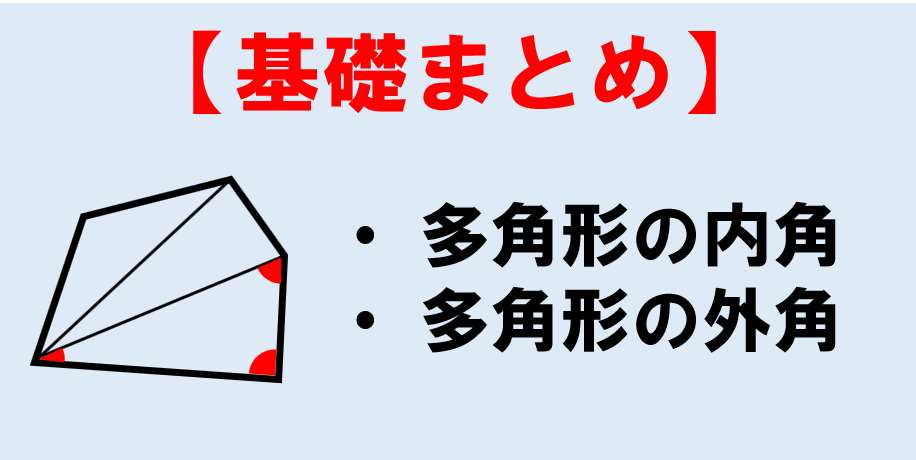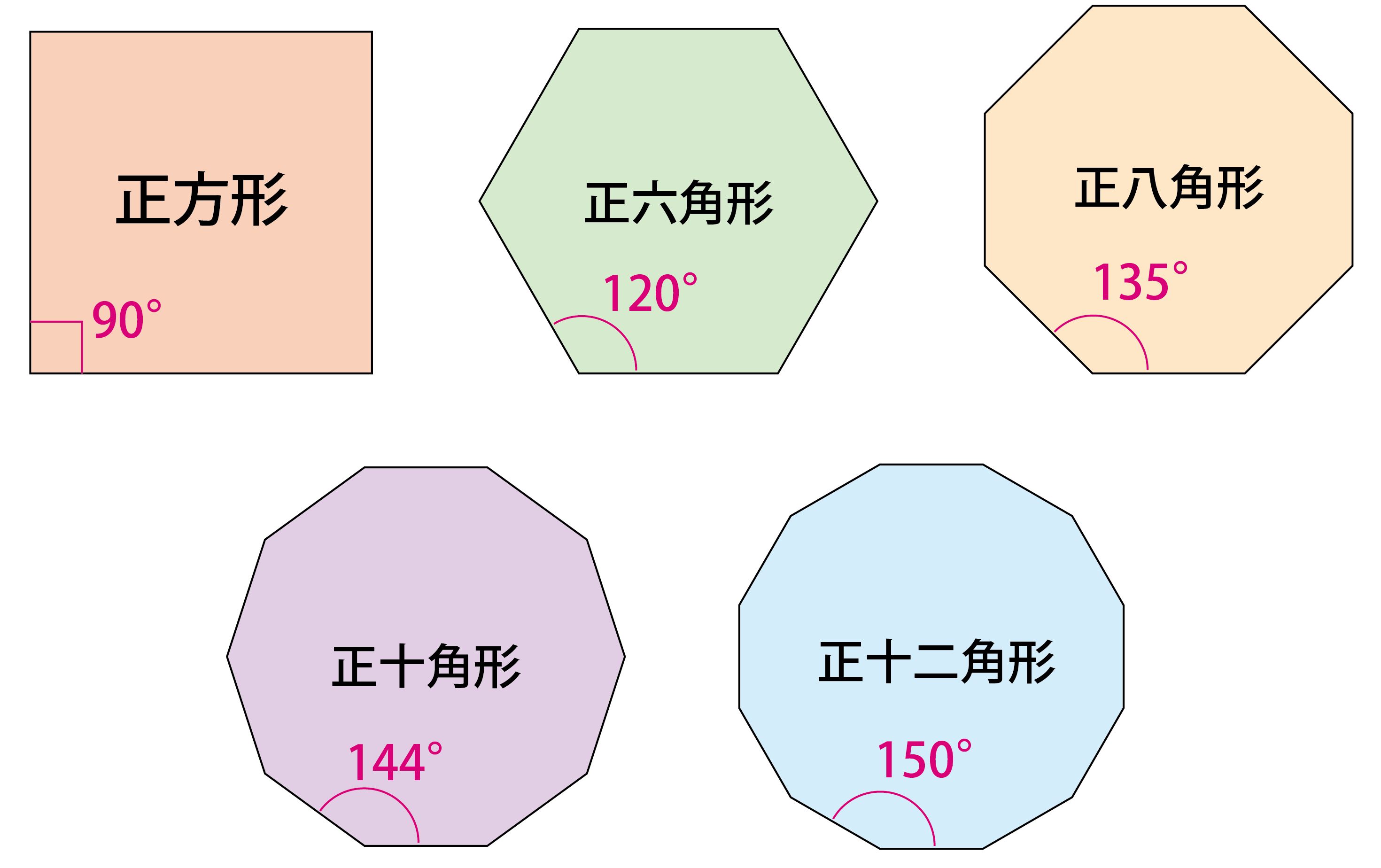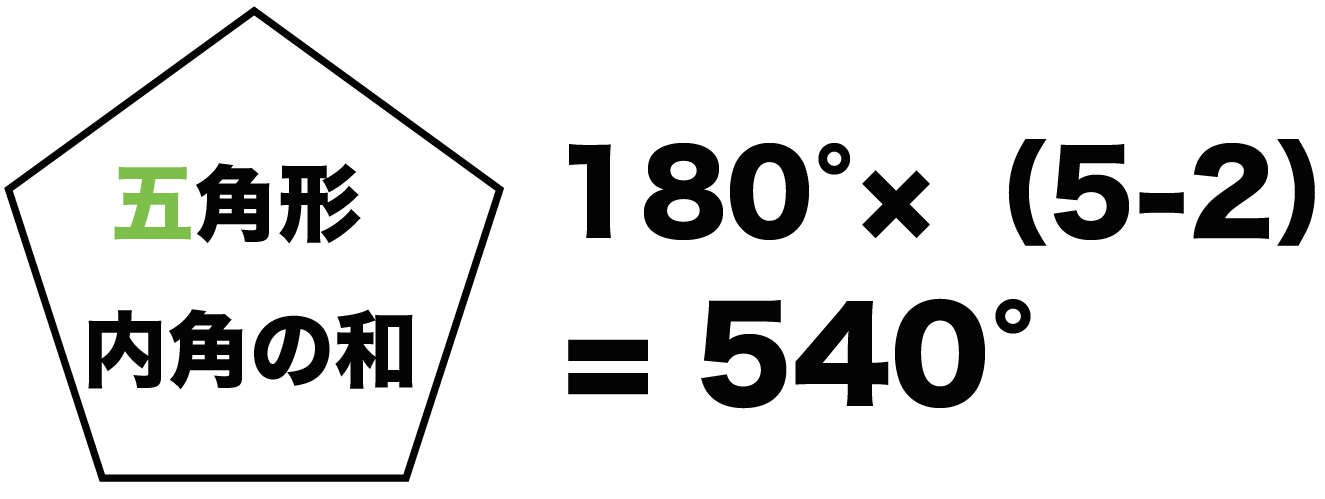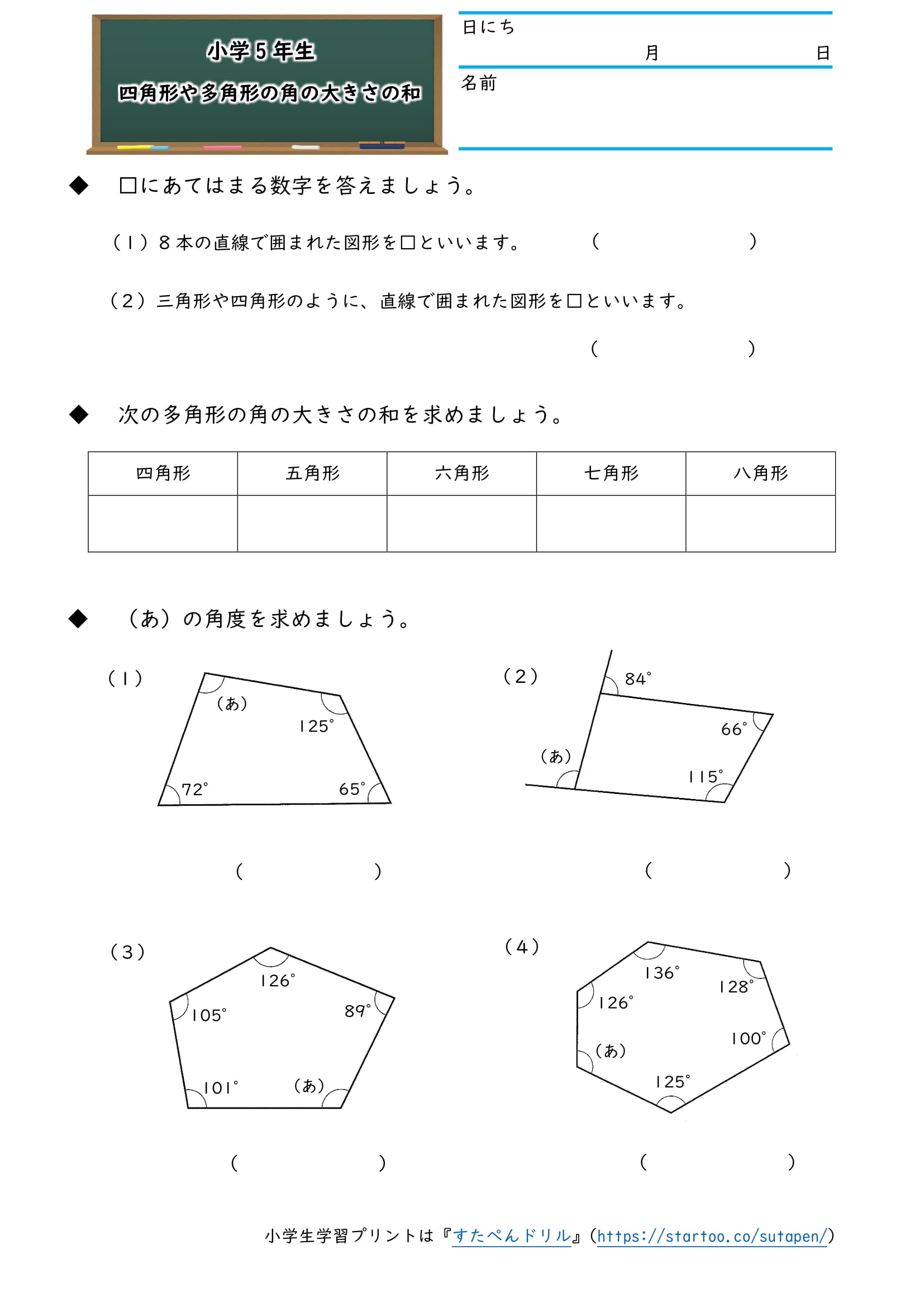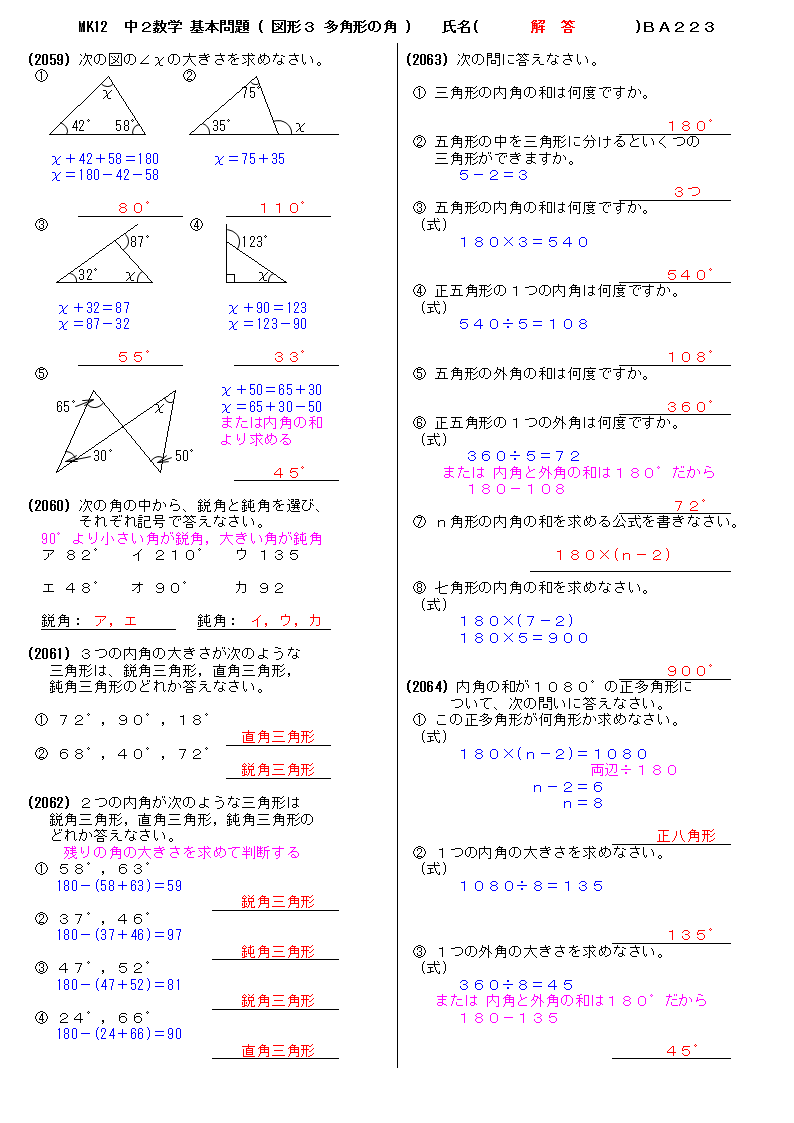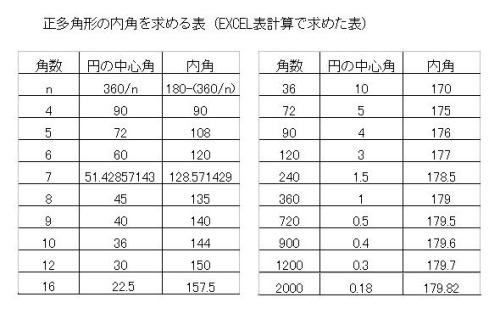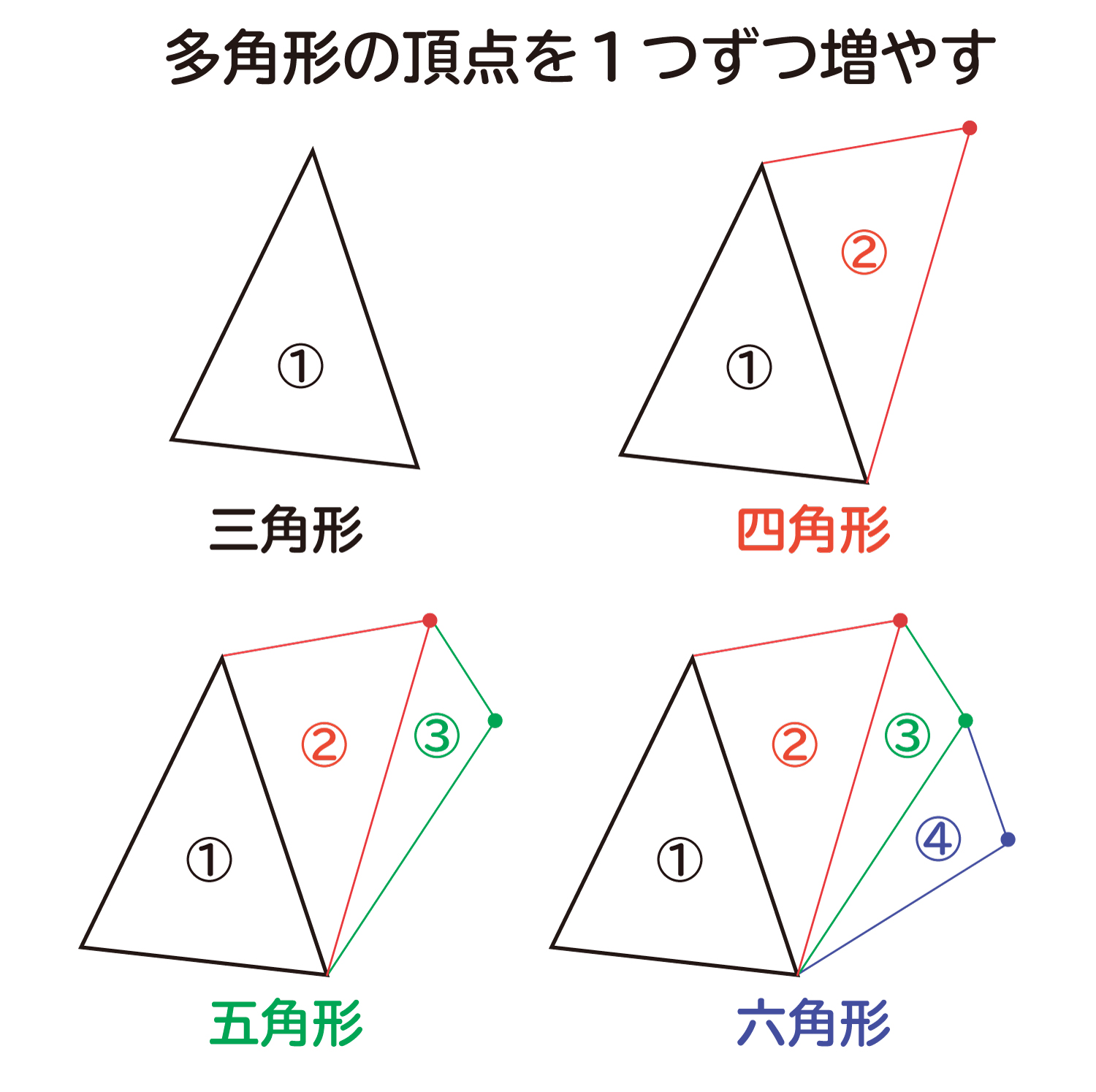 特別な多角形の内角の和 まなびの学園 |  特別な多角形の内角の和 まなびの学園 |  特別な多角形の内角の和 まなびの学園 |
 特別な多角形の内角の和 まなびの学園 |  特別な多角形の内角の和 まなびの学園 | 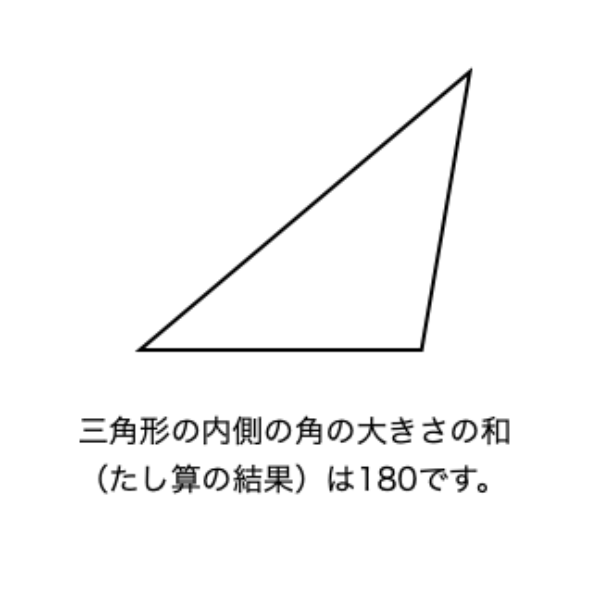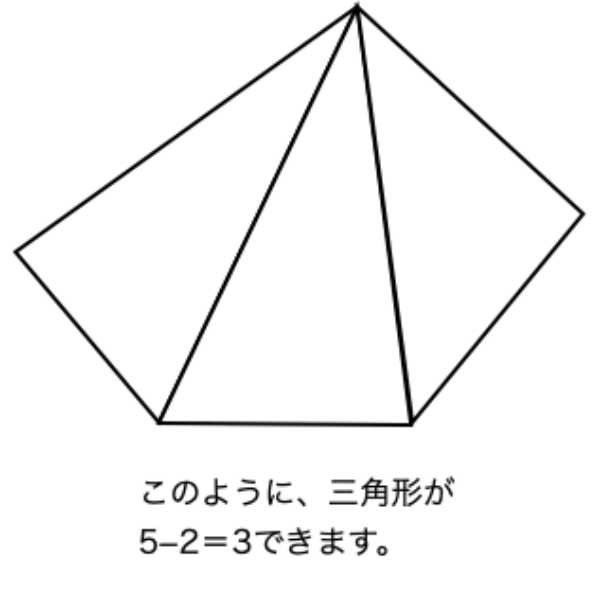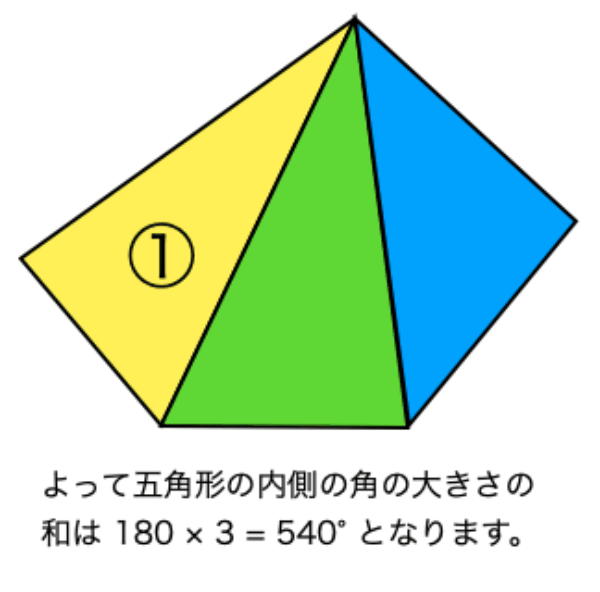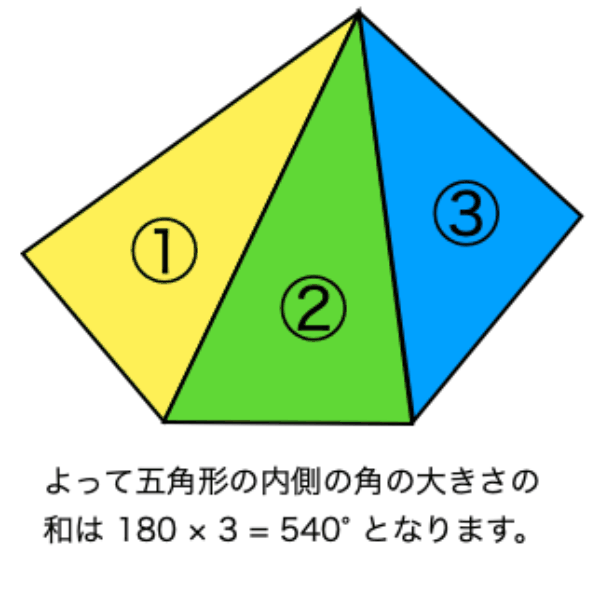 特別な多角形の内角の和 まなびの学園 |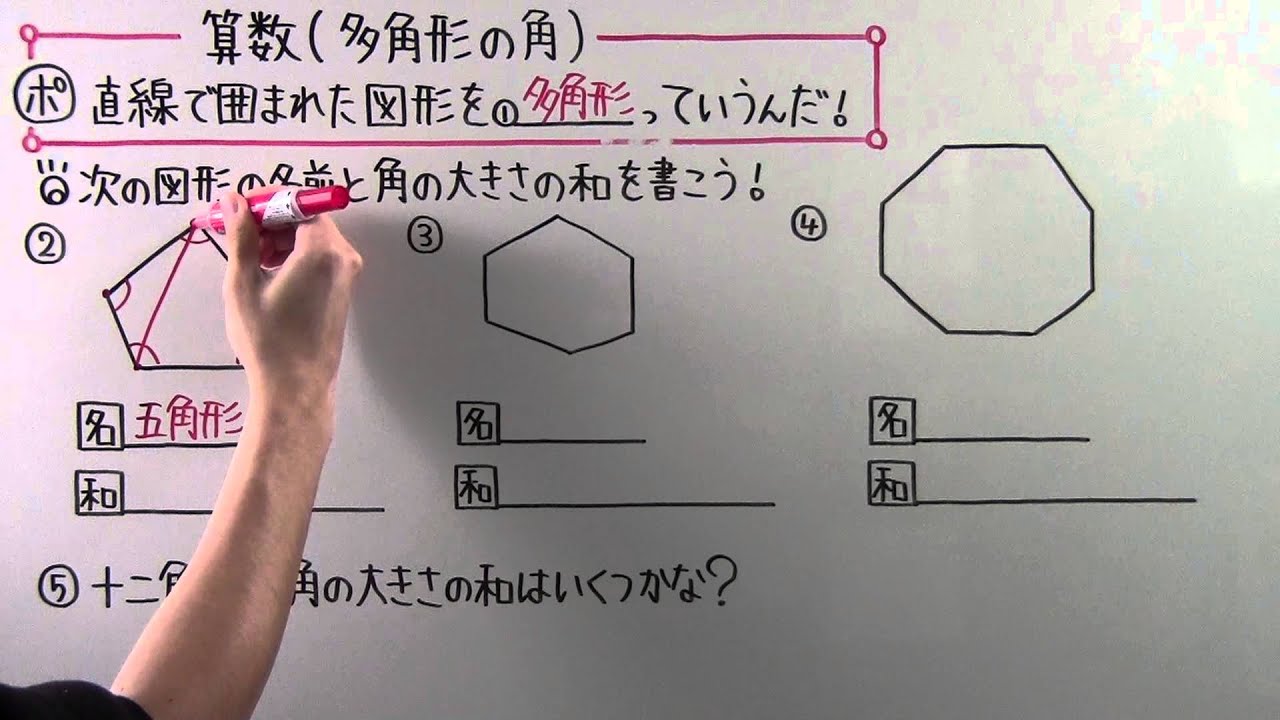
特別な多角形の内角の和 まなびの学園 |  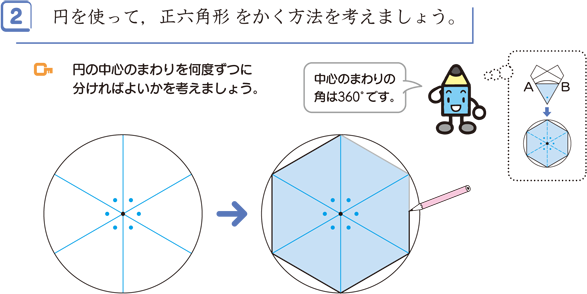特別な多角形の内角の和 まなびの学園 | 特別な多角形の内角の和 まなびの学園 |
「多角形の角の大きさの和の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 特別な多角形の内角の和 まなびの学園 |  特別な多角形の内角の和 まなびの学園 | 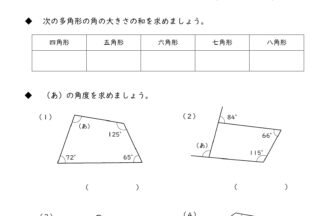 特別な多角形の内角の和 まなびの学園 |
 特別な多角形の内角の和 まなびの学園 | 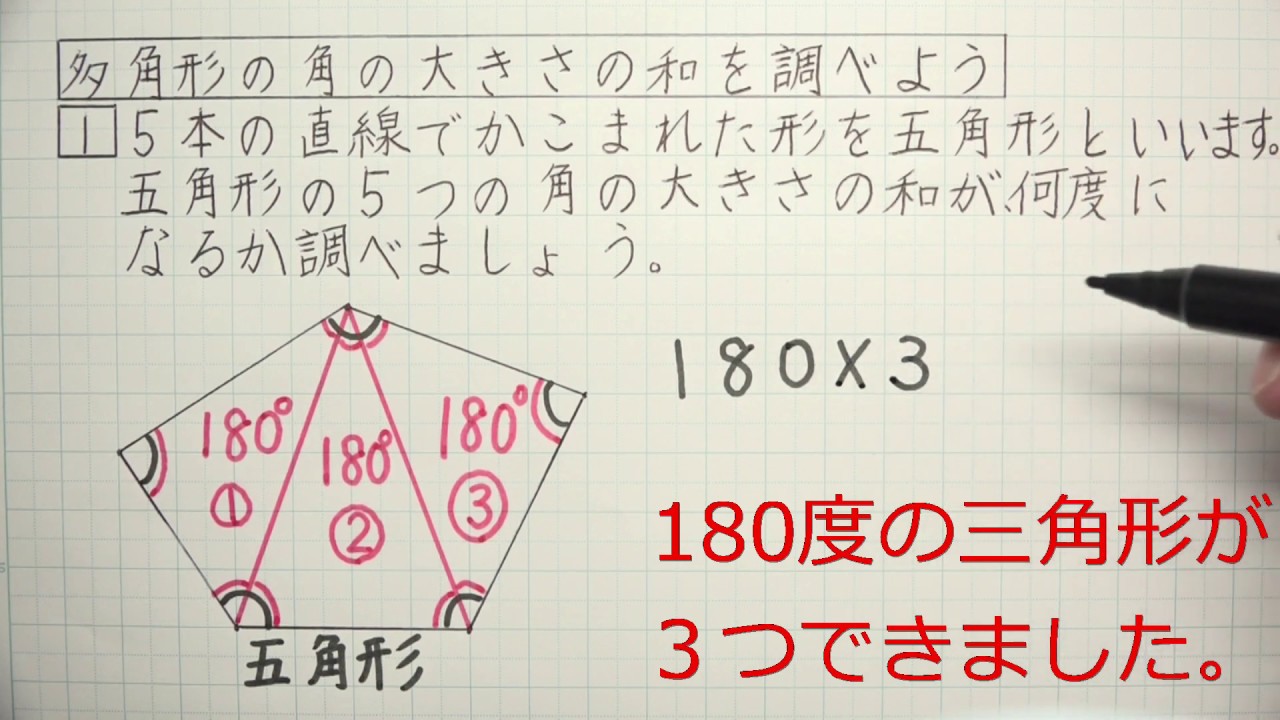 特別な多角形の内角の和 まなびの学園 |  特別な多角形の内角の和 まなびの学園 |
 特別な多角形の内角の和 まなびの学園 |  特別な多角形の内角の和 まなびの学園 | 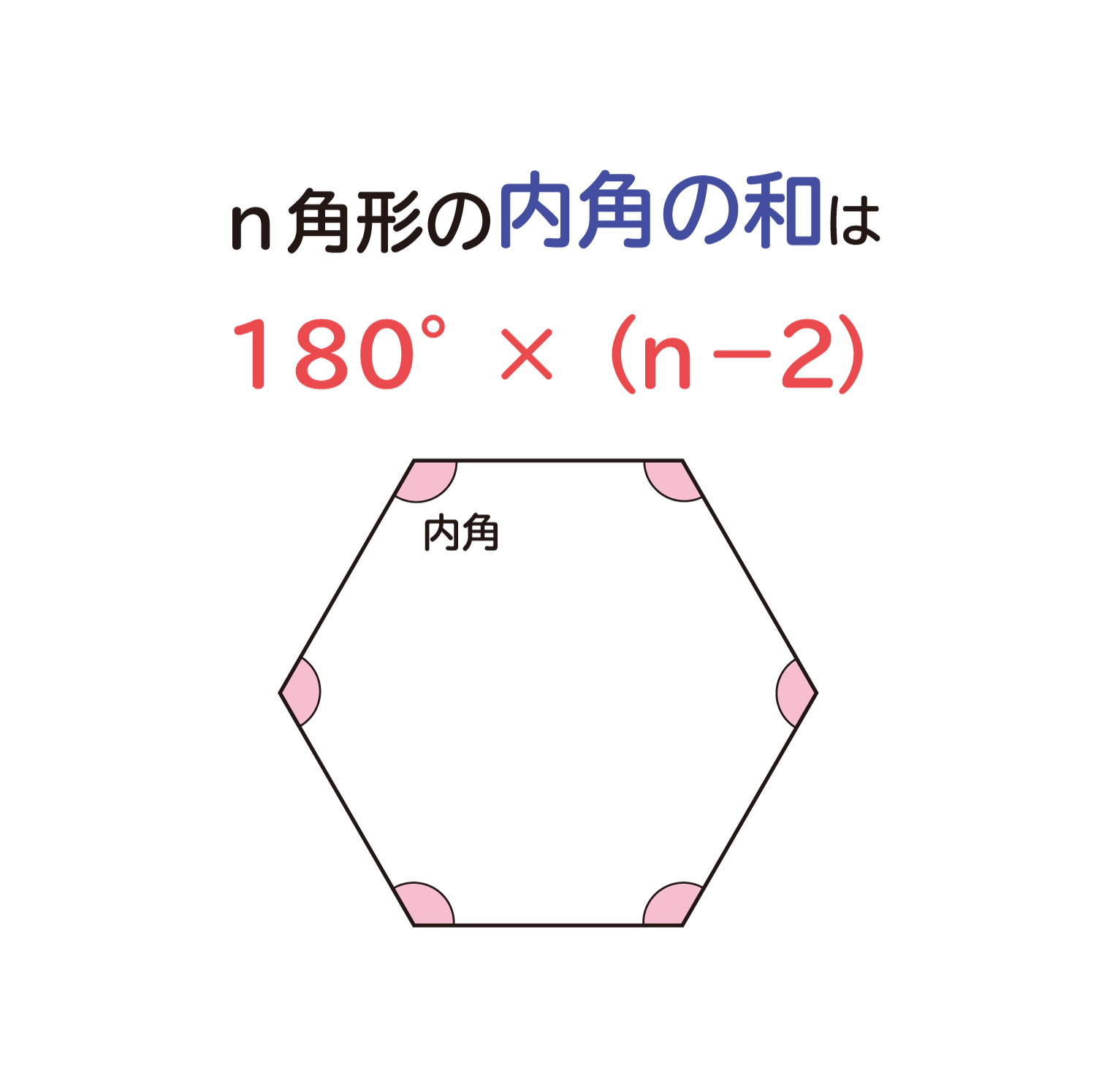 特別な多角形の内角の和 まなびの学園 |
「多角形の角の大きさの和の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 特別な多角形の内角の和 まなびの学園 | 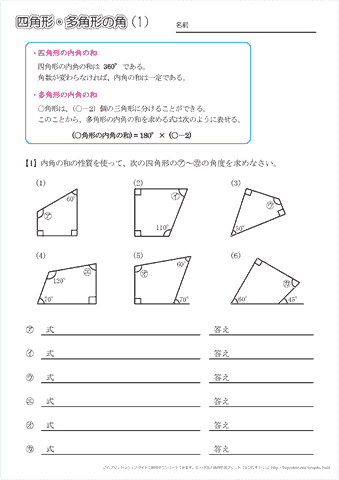 特別な多角形の内角の和 まなびの学園 | 特別な多角形の内角の和 まなびの学園 |
 特別な多角形の内角の和 まなびの学園 |  特別な多角形の内角の和 まなびの学園 | 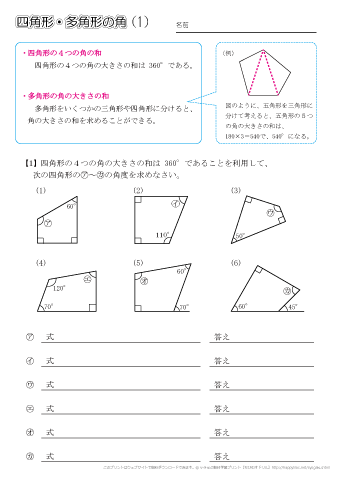 特別な多角形の内角の和 まなびの学園 |
 特別な多角形の内角の和 まなびの学園 |  特別な多角形の内角の和 まなびの学園 |  特別な多角形の内角の和 まなびの学園 |
「多角形の角の大きさの和の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 特別な多角形の内角の和 まなびの学園 |  特別な多角形の内角の和 まなびの学園 |  特別な多角形の内角の和 まなびの学園 |
 特別な多角形の内角の和 まなびの学園 |  特別な多角形の内角の和 まなびの学園 |
主要な多角形の面積の公式について解説していきます。 三角形の面積 まず、三角形の面積の公式を紹介します。 三角形の面積の公式 底辺 × 高さ ÷ 2 底辺を 、高さを とおくと、三角形八角形の内角の和は1080度である。 項目を8本の放射線に分けて、8つの項目の大小を対比する図表を、「オクタゴンチャート 要曖昧さ回避 」という。;
Incoming Term: 多角形の角の大きさの和, 多角形の角の大きさの和の求め方, 多角形の角の大きさの和 小学生,
コメント
コメントを投稿