[10000ダウンロード済み√] 面積比公式 293698-相似 面積比公式

淺談 三角形面積公式 Hackmd
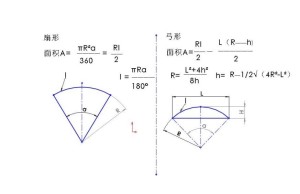
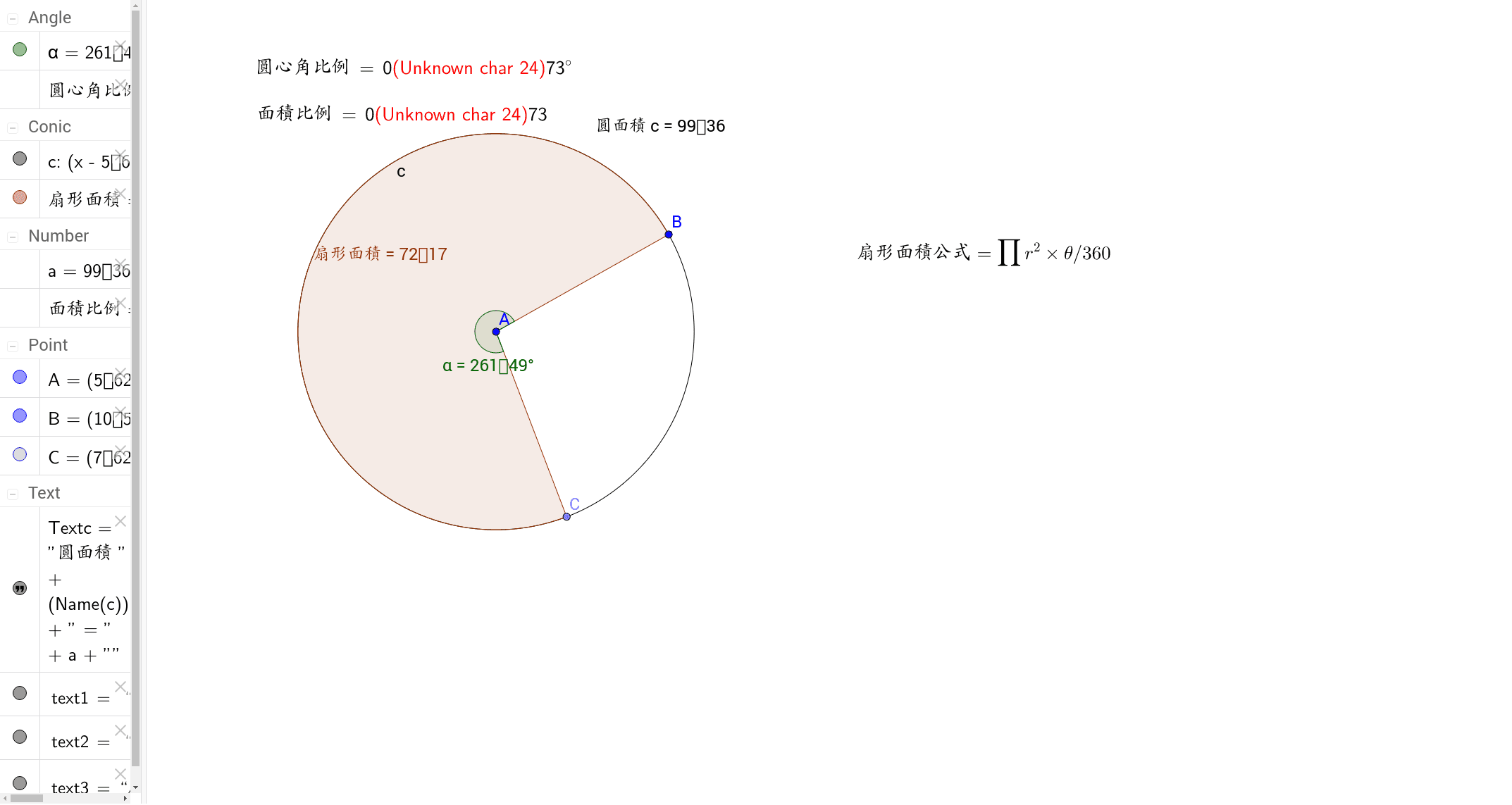
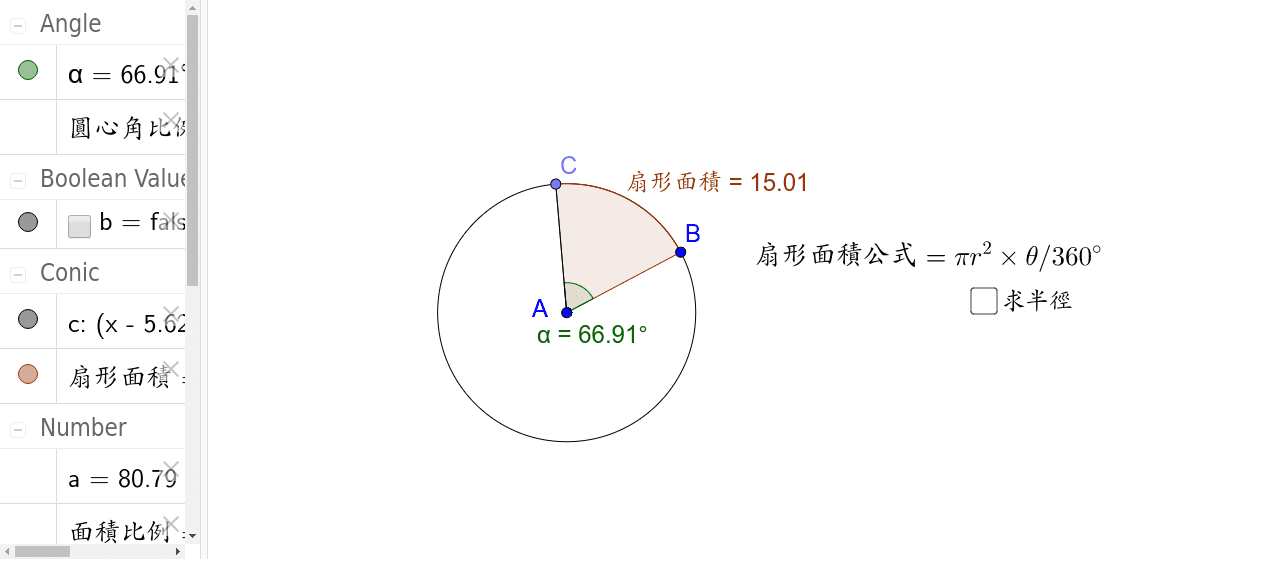
公式の導き方 扇形は円の一部分を切り取った図形です。扇形の面積は、「半径が等しい扇形の面積は、中心角に比例する」という性質を使って、円の面積 $\pi r^2$ に$ \frac{\text{中心「面積比」は「相似比の2乗」と等しい 例1 2つの三角形が相似で相似比が 12 1 2 のとき,面積比は, 1^22^2=14 12 22 = 1 4 になる。 このように, 相似比が ab a b なら 面積比は a^2b^2 a2 b2 に
相似 面積比公式
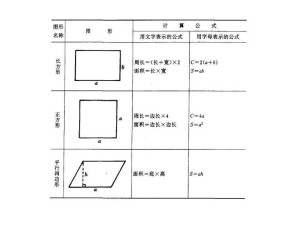
相似 面積比公式- 三角比5 (180°θ)型の変換公式はめっちゃ簡単! 前回の記事 では単位円を使って 0 ∘ ≦ θ ≦ 180 ∘ のときの三角比 sin θ, cos θ, tan θ を定義しました. これによって,例えば次のような問 面積公式一覧 三角形の面積=底辺×高さ÷2 正方形の面積=1辺×1辺。 長方形の面積=横×縦。 平行四辺形の面積=底辺×高さ。 台形の面積= (上底下底)×高さ÷2 ひし形の面積=対角

相似三角形面积比 无追搜索
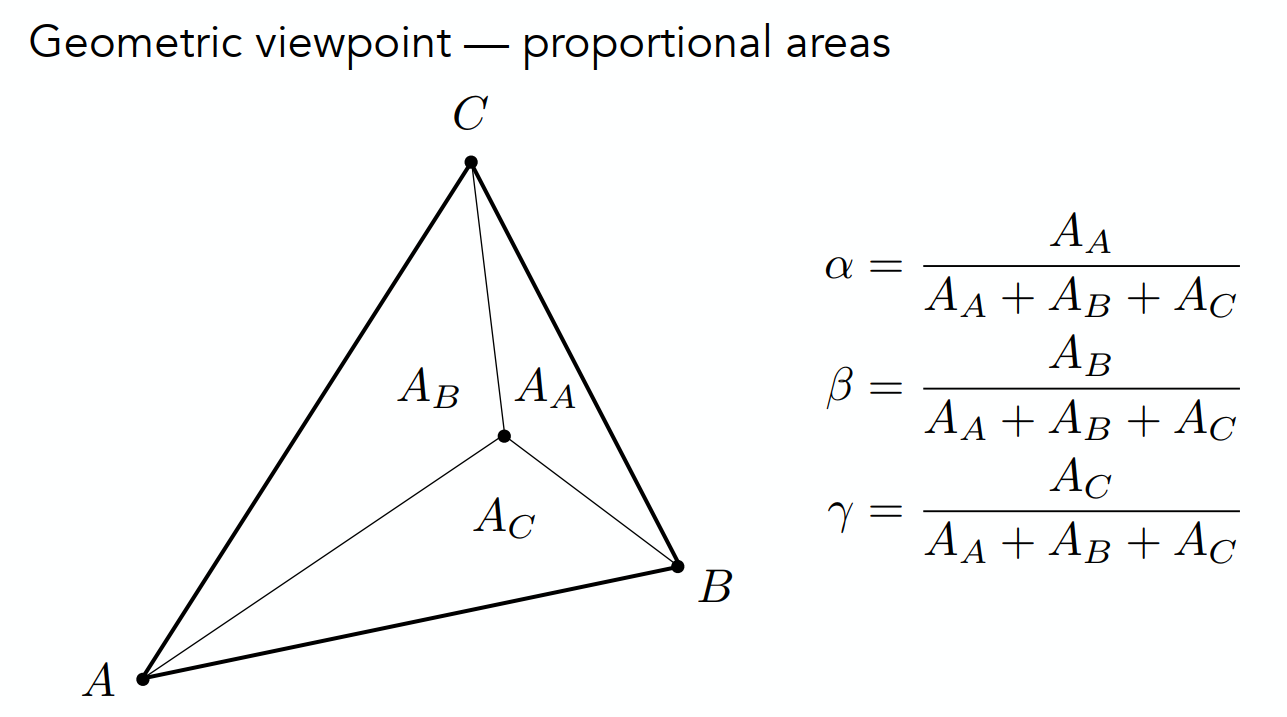
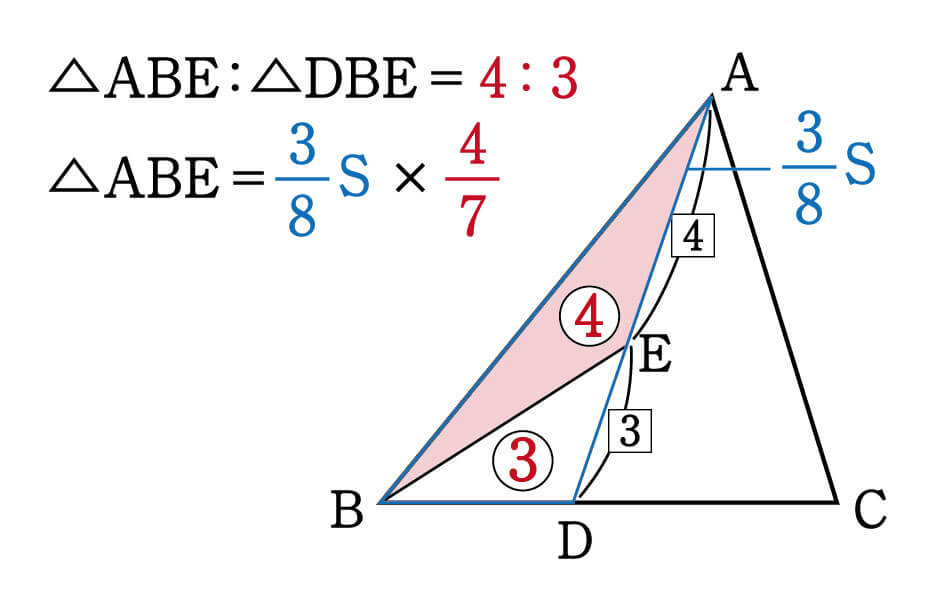
上野竜生です。三角形の面積を三角比で解く方法について考えていきたいと思います。 三角形の面積の公式 2辺の長さがa,bでその間の角がθである三角形の面積をSとするとき \( 1つ目のステップでは、 ABDと ACDの面積比に注目します。 隣り合う三角形の ①の型 なので、底辺の比=3:5から面積比も3:5。 そして左側の ABDは、 ABCを8等分したうちの3つ分 面積比の標準練習問題(解説・解答) (1)の解説 AED≡ FECより、 AGDと BGFは相似比1:2の相似となる。 よって、面積は相似比の2乗=面積比より、1:4となる。 (2)の
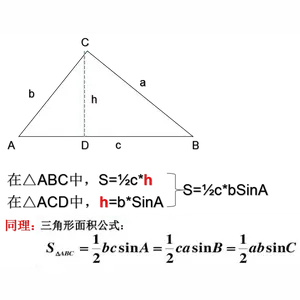
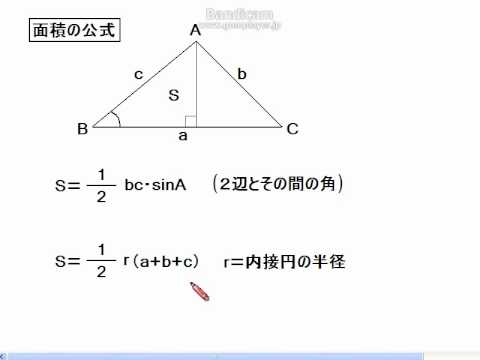
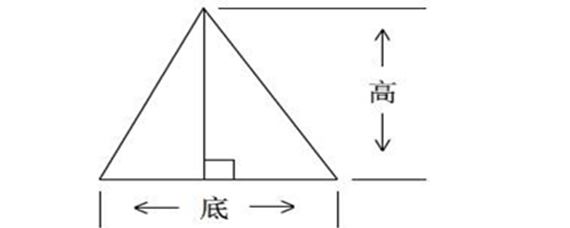
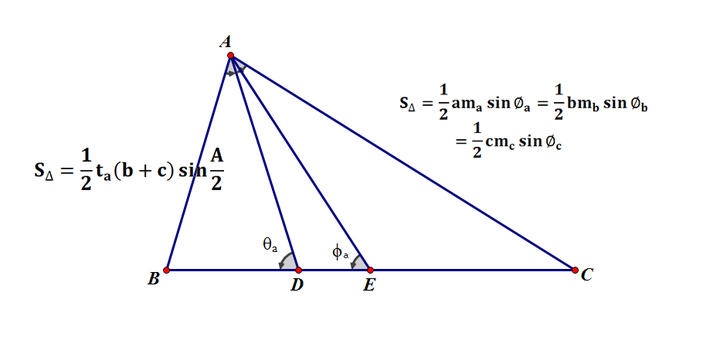
面積 = 底辺 × 高さ ÷ 2 正三角形 一辺の長さ a の三角形 一辺 いっぺん の長さ a a の三角形の面積 S S は、次の公式で求められます。 正三角形 せいさんかくけい の面積 S = √3 4 a2 S = 3 4 a 2 面積 このとき, ADHA A D H A と EDHE E D H E は相似なので, AHA EHE = AD ED= s t t A H A E H E = A D E D = s t t ABC A B C と EBC E B C の底辺を BC B C とみると,面積比は 三角比から三角形の面積を求める公式は、覚えておく必要がある超重要公式です。 三角形の面積の公式 三角形ABC 三角形の面積をSとすると、下記の式が成り立つ。 S = 1 2 a b sin C S
相似 面積比公式のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  |  |
 |  | |
「相似 面積比公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「相似 面積比公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 | ||
「相似 面積比公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「相似 面積比公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  | |
「相似 面積比公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  | |
「相似 面積比公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | ||
「相似 面積比公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  | |
「相似 面積比公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「相似 面積比公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「相似 面積比公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「相似 面積比公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |
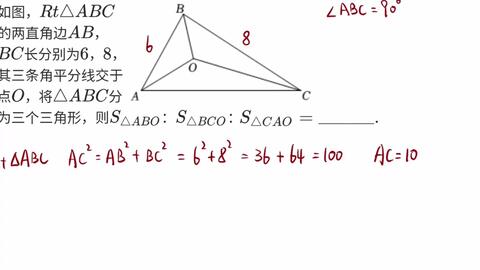
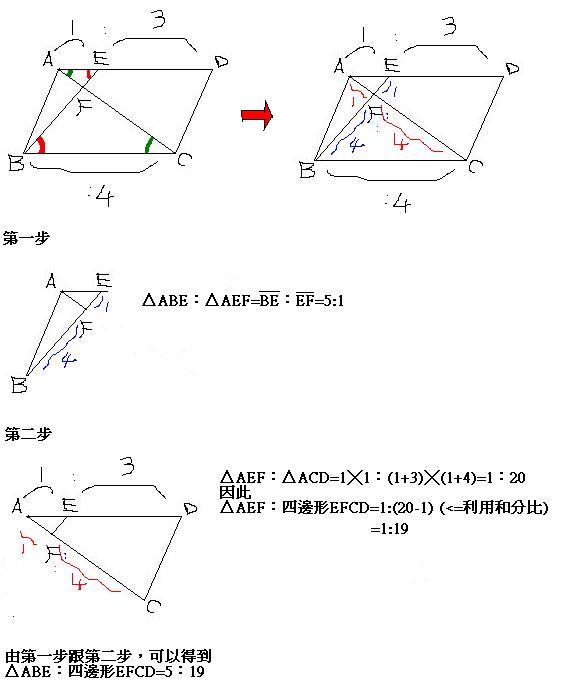
高さが等しいときには底辺の比が面積比と等しいのでaggf=813より、面積比は813である。 ≫ 次に aefと ebfを比べる。底辺をそれぞれae、ebとしたとき高さが共通なので 面積比はaeebの比と同 辺の比が分かっているので、面積比も求めることができます。 三角形 の面積を とすると、 BD DC = 5 4 なので、三角形 の面積は 5 9 S 、三角形 の面積は 4 9 S となります。 さらに、
Incoming Term: 面積比公式, 相似 面積比公式,
コメント
コメントを投稿